004. HOLOGRAM

1. 홀로그램의 세계
우리가 사는 이 현상계는 빛의 파장에 의한 보는 자의 세계이고 실체는 텅빈 공간
으로 하나의 완벽한 가상 현실(HOLOGRAM)이라는데 동의 할 수 있읍니다.
따라서 분자 원자 까지 다 볼 수 있는 고성능 전자 현미경 같은 눈을 사람들이 가졌
다면 사람들 모습이 텅 빈 허공 속에 파동으로 이어진 의식체로 보일테고 그 모습
들은 유령이나 다를 바 없을 것입니다.
더 나아가 원자의 양성자 중성자 전자 까지 볼 수 있는 눈이라면 초 소립자들의 있
고 없음이 10(-23승)초 사이로 반복되는 현상 까지 볼 수 있다면 사람 형상 자체를
있다고 할 것인지 없다고 할 것인지 우리 눈이 느끼는 감각 수준이 지금 우리가 볼
수 있는 대상의 크기와 정밀도에 맞춰져있고, 가시광선의 빛의 파장으로 구별 할
수 있기에 모든 사물이 지금같이 보일뿐 입니다.
사람이 보는 장미꽃은 주먹만 하지만 꿀벌에게는 백배이상 큰 크기로 보게 되니
모든 것이 보는 자의 인식 능력과 자신의 몸 크기에 따라 각각 다르게 보이는 것입
니다.
빛의 파장등 특정한 조건, 자신의 몸과 인식의 크기에서 보이고 느껴지는 현상계
가 전부이고 실재인양 살고 있는 허상속의 중생들도 이 홀로그램 같은 가상의 세
계가 허상에 불과 하다는 것을 알고 빠져나가서 그 허상 세계를 나투어 낸 초 의식
세계인 우주허공 眞空妙有 자리에서 거듭난다면 중생도 해탈하여 부처가 되고 실
상세계에서 生死一如, 有無情이 하나로 영생 할수 있을 것입니다.
이렇듯 홀로그램은 너무나 기이해서 과학적 이해의 영역 밖으로 제쳐 놓았던 광
범위한 현상들이 갑자기 이해되기 시작했다는 점 들이며, 텔레파시, 예시, 우주와
의 신비한 일체감, 심지어는 염력현상, 마음으로 움직이는 능역까지도 설명이 된
다는 것이다. 또한 홀로그램을 중시하는 이유는 홀로그램의 모든 부분이 전체상을
담고 있는 것과 똑같이 우주의 모든 부분이 전체를 품고 있다는 것이다. 즉 전체가
개체요 개체가 전체이다라는 말로 바꿀 수 있다.
<윌리암 브레이크의 시>
한 알의 모래 속에서 우주를
들 꽃 속에서 천국을 보려거든
그대의 손바닥 속에서 무한을
한 시간 속에서 영겁을 붙잡아라

2. 홀로그램의 두뇌: 기억의 막대한 용량
헝가리 태생의 물리학자인 존 폰 노이만(John von Neumann)은 인간의 평균수명
동안에 두뇌는 자그만치 2.8x10^20(280,000,000,000,000,000,000)비트(bit)의 정
보를 기억한다는 것을 계산해 냈읍니다. 이것은 어마어마한 양의 정보입니다.
두뇌 연구자들은 이같이 엄청난 용량을 설명해줄 매카니즘을 밝혀내기 위하여 오
랫동안 씨름 해왔읍니다.
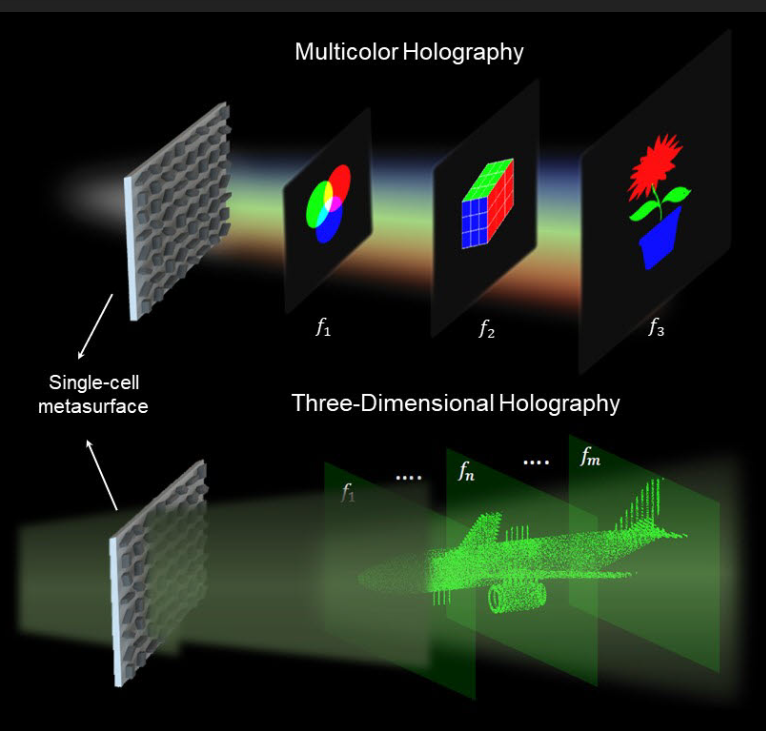
흥미롭게도 홀로그램 또한 정보를 저장하는 대단한 용량을 지니고 있읍니다.
2개의 레이저 광선이 필름에 부딪치는 각도를 변화 시키면 동일한 필름 표면에 서
로 다른 이미지를 기록하는 것이 가능한 것입니다.
그렇게 기록된 이미지는 단지 원래의 레이저 광선의 각도와 동일한 각도로 필름을
비추기만 하면 재생해낼 수 있읍니다.
학자 들은 이 방법을 사용하면 1제곱 인치 크기의 필름 속에 성경책 50권에 해당
하는 분량의 정보를 저장할 수 있음을 계산 해냈읍니다.
3. 홀로그램 두뇌 설을 뒷 바침하는 실험
인디애나 대학의 생물학자 폴 피치(Paul Pietsch)는 일련의 실험을 행하였는데
실험 대상으로 도룡뇽을 택 했읍니다.
도롱뇽을 죽이지 않고 뇌를 제거할 수 있었으며 두뇌가 없는 동안에는 혼수상태
가 되었지만 그것을 회복 시키면 곧바로 완전히 정상으로 되돌아 왔읍니다.
피치는, 만일 도룡뇽의 먹이 습성이 뇌의 특정한 위치에 국소적으로 자리 잡고
있지 않다면 도룡뇽의 먹이 습성은 뇌가 머리 속에서 어떻게 위치해 있는가 와는
무관해야 한다고 생각했읍니다.
그래서 그는 도룡뇽의 좌뇌와 우뇌를 뒤바꾸어 놓았고, 도룡뇽은 회복되자마자
곧 정상적인 먹이습성을 보였읍니다. 또 다른 도룡뇽을 택하여 아래위를 바꾸어
보았읍니다.
역시 뇌가 회복되자 정상적으로 먹이를 먹었으며, 그래서 더 과격한 방법으로
100회가 넘게 시험을 행하였는데 이 운 나쁜 동물의 뇌를 얇게 썰고, 뒤집고, 버
무리고 심지어는 잘게 저 몃 읍니다.
그러나 뇌를 되 갖다 놓을 때마다 도룡뇽의 행동은 정상으로 돌아 왔읍니다.
그의 연구는 TV취재물인 <60분>에 방영 되었읍니다.

4. 홀로그램의 수학적 언어
홀로그램 개발을 가능케한 이론은 데니스 가르보(Dennis Gabor; 그는 이공로로
노벨상을 수상) 그는 수학적 접근법을 사용 했읍니다.
그가 사용한 수학은 18세기 수학자 쟝B.J.푸리에(JeanB.J.Fourier)가 고안한 계산
법 이었읍니다.
푸리에가 고안한 방법은 아무리 복잡한 패턴이라도 그것을 단순한 파동의 언어로
변환 시키는 수학적 방법으로서 이 파동형태가 다시 원래의 패턴으로 변환 될수 있
음을 보여주었읍니다.
달리 말해서, TV 카메라가 영상을 전자기파로 변환 시키고 TV수상기는 이 파동을
원래의 영상으로 변환 시키듯이 이와 비슷한 과정으로 수학적으로 해 낼 수 있는
방법을 제시 한 것입니다.
이 푸리에 변환 식 덕분에 가르보는 피사체의 이미지를 변환시켜 홀로그램 필름위
의 간섭무늬 자국으로 바꾸어 놓을 수 있었으며 다시 원래의 대상의 이미지로 변환
시킬 수 있었읍니다.
1979년 버클리 대학의 신경생리학자 러셀과 카렌 드발로아(Russell and Karen
DeValois)부부에 의해 시신경계가 일종의 주파수 분석기로 작용한다는 것을 시험
하였읍니다.
푸리에 변환식을 사용하여 격자무늬와 바둑 판 무늬를 단순한 파형으로 변환시켜
시각피질의 뇌세포가 이 새로운 파형 이미지에 어떻게 반응 하는지를 시험한 결과
뇌세포는 원래의 패턴이 아니라 푸리에방정식으로 변환된 패턴에 반응 한다는 것
을 결론지었으며 두뇌는 홀로그램 사진술이사용하는 것과 동일한 푸리에 수학을
사용하여 시각적 이미지를 푸리에의 파형언어로 변환 시킨 것입니다.
이후 귀, 후각, 피부, 혀등 모두 수학 방정식 푸리에 방정식의 형식임을 발견
하였읍니다.
'일상의 삶' 카테고리의 다른 글
| 006. 양자역학[量子力學[quantum mechanics] (69) | 2024.11.17 |
|---|---|
| 005. 數이야기 (42) | 2024.11.15 |
| 003. Bee CAM (73) | 2024.11.11 |
| 002. 신과 메아리 (51) | 2024.11.09 |
| 001. 김치에 대하여 (104) | 2024.10.04 |



