007. 프랙탈이론
프랙탈 이론에 대해 자세히 알아보겠습니다. 프랙탈은 자연에서 발견되는 복잡
한 구조를 설명하는 수학적 개념으로, 자기유사성과 반복성을 특징으로 합니다.
이 글에서는 프랙탈 이론의 정의부터 역사, 주요 개념, 예시, 응용, 카오스 이론과
의 관계, 그리고 미래에 대해 체계적으로 설명하겠습니다.
1. 프랙탈 이론의 정의
프랙탈은 부분이 전체와 유사한 기하학적 형태를 의미합니다. 이러한 자기유사성
은 자연에서 흔히 발견되며, 나무의 가지, 구름의 형태, 그리고 해안선의 모양 등에
서 그 예를 찾아볼 수 있습니다. 프랙탈 이론은 이러한 복잡한 구조를 수학적으로
설명하고 분석하는 데 도움을 줍니다.
2. 프랙탈의 역사
프랙탈 이론은 1970년대에 수학자 벤오프(Benoit Mandelbrot)에 의해 본격적으
로 연구되었습니다. 그는 프랙탈을 통해 자연의 복잡성을 설명할 수 있는 새로운
방법을 제시하였고, 그의 연구는 다양한 분야에 큰 영향을 미쳤습니다. 프랙탈 이
론은 이후 컴퓨터 그래픽스, 물리학, 생물학 등 여러 분야에서 활용되고 있습니다.
3. 프랙탈의 주요 개념
프랙탈의 핵심 개념은 자기유사성과 반복성입니다. 자기유사성은 작은 부분이 전
체와 유사한 형태를 가지는 것을 의미하며, 반복성은 간단한 규칙을 통해 복잡한
구조를 생성하는 과정을 설명합니다. 이러한 개념은 프랙탈의 아름다움과 복잡성
을 이해하는 데 중요한 역할을 합니다.
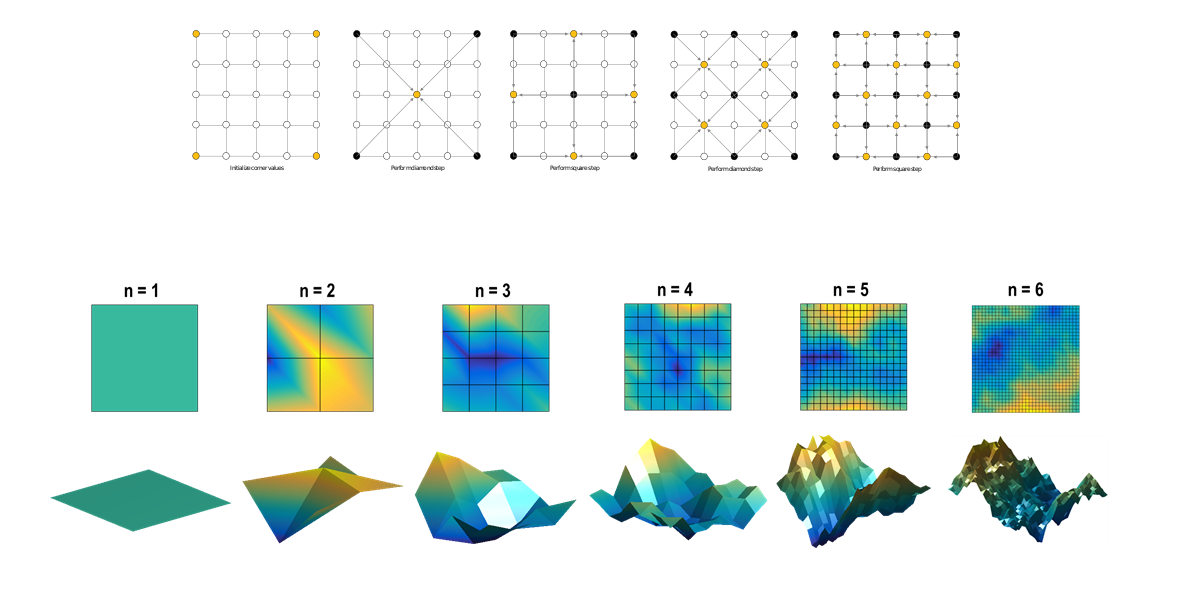
4. 프랙탈의 예시
프랙탈의 대표적인 예시로는 로렌츠 어트랙터(Lorenz attractor)가 있습니다. 이
구조는 복잡한 나비 모양을 형성하며, 초기 조건에 민감한 카오스적 행동을 보여줍
니다.

이 와 함께 다양한 프랙탈 패턴들이 존재하는데, 그 중 하나는 화려한 색상 그라데이션을
가진 프랙탈 패턴입니다.

이러한 패턴들은 수학적 규칙에 따라 생성되며, 대칭성과 혼돈을 동시에 보여줍니다.
또한, 여러 가지 프랙탈 패턴을 비교할 수 있는 이미지도 있습니다.

이 이미지는 서로 다른 프랙탈 구조를 보여주며, 각기 다른 복잡성과 반복성을 가
지고 있습니다.
프랙탈 구조는 자연에서도 쉽게 찾아볼 수 있습니다. 예를 들어, 나무의 가지는 프
랙탈 구조를 가지고 있으며, 이는 두 차원 확산 제한 집합(DLA) 패턴을 통해 설명
될 수 있습니다.

이와 함께 나무의 가지를 강조한 그래프도 포함되어 있습니다.
5. 프랙탈 이론의 응용
프랙탈 이론은 다양한 분야에서 응용되고 있습니다. 예를 들어, 컴퓨터 그래픽스
에서는 프랙탈을 이용하여 자연의 복잡한 형태를 시뮬레이션할 수 있습니다.
또한, 생물학에서는 세포 구조의 복잡성을 이해하는 데 도움을 주며, 물리학에서
는 카오스 이론과의 관계를 통해 복잡한 시스템을 분석하는 데 사용됩니다.
6. 프랙탈과 카오스 이론의 관계
프랙탈 이론과 카오스 이론은 밀접한 관계가 있습니다. 카오스 이론은 복잡한 시
스템의 예측 불가능한 행동을 연구하는 분야로, 프랙탈은 이러한 시스템의 구조적
특성을 설명하는 데 중요한 역할을 합니다. 예를 들어, 프랙탈 구조는 카오스적 행
동을 나타내는 시스템에서 자주 발견됩니다.
이러한 관계는 복잡한 시스템을 이해하는 데 필수적입니다.
7. 프랙탈 이론의 미래
프랙탈 이론은 앞으로도 다양한 분야에서 계속 발전할 것으로 기대됩니다. 특히,
인공지능과 머신러닝의 발전으로 인해 프랙탈 이론의 응용 가능성이 더욱 확대될
것입니다. 또한, 자연 현상을 이해하는 데 있어 프랙탈 이론은 중요한 도구로 자리
잡을 것입니다.
프랙탈 이론은 단순한 수학적 개념을 넘어, 자연의 복잡성을 이해하는 데 큰 도움
을 주고 있습니다. 앞으로도 이 이론이 어떻게 발전해 나갈지 기대가 됩니다.
8. 화엄경
불교 가르침의 최고봉이라고 하는 화엄경에는 우주의 모습이 기술되어 있습니다.
그런데 그 내용이 놀랍도록 정확하게 '프랙탈적'입니다
화엄경에는 부처님이 삼매에 들었을 때 이 세상의 모습이 여러 번에 걸쳐 묘사 되
는데, 그 내용은 이러합니다.
부처님이 삼매에 들면 몸에서 광명(光明)이 뿜어져 나오고, 이 광명은 우주 법계
속으로 끝없이 뻗어 나갑니다. 이 광명이 뻗어 나가면 어두운 우주가 밝아지는데,
그 빛이 비추이는 우주 곳곳에는 우리가 사는 것과 같은 세계가 무한히 존재하며,
그 세계마다 부처님이 계셔서 똑같은 가르침을 설하고 있습니다. 그리고 부처님
옆에 구름처럼 모인(雲集) 모든 중생들은 부처님의 위신력에 의해 부처님과 똑같
은 삼매에 들어 그 광경을 목격합니다.
이런 우주의 모습을 화엄경은 '중중무진법계(重重無盡法界)'라고 말합니다.
또 화엄경은 '한 티끌 속에 모든 우주가 들어 있고(一味塵中含十方) 무량한 시간
이 한 생각에 다 들어있다(無量遠怯則一念)' 고 이야기합니다. 그런데 이 말들, 즉
하나에 모든 것이 있고 한 생각이 바로 무량한 시간이라는 말도 프랙탈 이론으로
생각하면 틀림없는 사실이 됩니다. 하나(一)가 다중(多重)이 되며 다중은 또한 하
나에 드는 것이다. 부처님도 예수님도, 비록 그 분들은 유한한 시간, 유한한 공간
속에 유한한 삶을 사셨지만, 프랙탈 이론으로 보면 영원한 시간, 영원한 공간을
사는 것 이된다.
<물리학에서는 물리학자 갈릴레이가 근대 과학을 열었으며 물리학자 뉴턴은 그
것을 이어받아서 고전 역학을 완성했다. 뉴턴의 학문은 결정론을 대변하며 뉴턴
의 운동 법칙은 화살의 비행 궤도와 나무에서 떨어지는 원숭이의 낙하 궤도를 정
확히 예측한다. 화살과 원숭이가 몇 초 후 어느 위치에 있을지를 명확히 파악할
수 있는 것이다. 이뿐이 아니다. 뉴턴의 운동법칙은 몇 시간 후, 며칠 후의 인공
위성과 우주선의 궤도를 결정해준다. 이것이 뉴턴의 결정론이다.
결정론은 만병통치약일 줄 알았다. 자연 현상의 미래는 물론이고, 초기 상태만 완
벽하게 주어지면 사회 현상의 변화무쌍함도 감히 예측 가능하다고 보았다.
하지만 그게 그렇지가 않았다. 뉴턴 결정론은 20세기 초 양자론이라는 현대물리
학의 큰 기둥을 만나면서 흔들렸다. 원자 내부라는 미시세계로 들어가자 자연 현
상의 완벽한 예측은 원천적으로 무리라는 사실이 드러났다.
그러다 보니 사회 현상 쪽으로의 접근은 더 더욱이나 요원한 일로 여겨졌으나,
20세기 중반에 이르러 이를 보완할 수 있는 길이 보이기 시작했다. 이것이 폴란
드 출신의 미국 과학자 만델브로(Benoit Mandelbrot)가 프랙탈(Fractal)이론 인
것이다.>
8. 참고자료
[1] 네이버 블로그 - [정보] 프랙탈 이론 (Fractal) - 네이버 블로그 - NAVER (https://m.blog.naver.com/jan_pona/222116729935)
[2] Wikipedia - 프랙탈 - 위키백과, 우리 모두의 백과사전 (https://ko.wikipedia.org/wiki/%ED%94%84%EB%9E%99%ED%83%88)
[3] NAVER - 프랙탈 이론과 카오스 이론
(https://blog.naver.com/eiaso/90181360402)
[4] 대순진리회 여주본부도장 - 세포 안에 우주가 있다 - 프랙탈 이론
(https://webzine.daesoon.org/board/readcnt.asp?bno=4323&win=new)